Exercices

Chapitre 2: Diviser pour régner

1 Algorithmes de tris quadratiques vus en première

Vous avez vu en première deux algorithmes de tris peu efficaces(complexité $O(n^2)$):

• Le tri par sélection

  Sur un tableau de n éléments (numérotés de $0$ à $n-1$), le principe du tri par sélection est le suivant :

  • Rechercher le plus petit élément du tableau, et l’échanger avec l’élément d’indice 0 ;
  • rechercher le second plus petit élément du tableau, et l’échanger avec l’élément d’indice 1 ;
  • continuer de cette façon jusqu’à ce que le tableau soit entièrement trié.   Source Wikipedia

• Le tri par insertion

  Dans l’algorithme, on parcourt le tableau à trier du début à la fin. Au moment où on considère le i-ème élément, les éléments qui le précèdent sont déjà triés. Pour faire l’analogie avec l’exemple du jeu de cartes, lorsqu’on est à la i-ème étape du parcours, le i-ème élément est la carte saisie, les éléments précédents sont la main triée et les éléments suivants correspondent aux cartes encore mélangées sur la table.

  L’objectif d’une étape est d’insérer le i-ème élément à sa place parmi ceux qui précèdent. En pratique, on fait « remonter » l’élément au fur et à mesure jusqu’à rencontrer un élément plus petit.

1. On considère la liste suivante de neuf valeurs: [36, 45, 36, 9, 15, 23, 11, 38, 40].

   Donner l’état de la liste à la fin des neuf étapes de tri pour le tri par sélection et le tri par insertion.

   Pourquoi l’algorithme a une complexité quadratique alors que la liste ne passe que par neuf états au cours de son tri?

2. Implémenter ces deux algorithmes de tri en Python:

   • tri_selection(tbl: list) -> list
   • tri_insertion(tbl: list) -> list

   Tester les fonctions avec les assertions suivantes:

   tbl = [36, 45, 36, 9, 15, 23, 11, 38, 40]
   assert tri_selection(tbl) == [9, 11, 15, 23, 36, 36, 38, 40, 45]
   assert tri_insertion(tbl) == [9, 11, 15, 23, 36, 36, 38, 40, 45]
   
   # avec des valeurs aléatoires
   import random as rd
   tbl =  [rd.randint(-1000, 1000) for i in range(1000)]
   # bien évidemment Python sait trier!
   trié = sorted(tbl)
   assert tri_selection(tbl) == trié
   assert tri_insertion(tbl) == trié

2 Rotation d’une image d’un quart de tour

Exercice inspiré du travail de Laurent Cheno, les images proviennent de son notebook que l’on ne peut plus trouver en ligne.

On considère l’image suivante de la Joconde découpée en carré de 1024x1024.

La Joconde carrée

Pour la réalisation de cet exercice, il est conseillé d’utiliser le package Python pillow.

Voici le code nécessaire à l’ouverture d’une image et à l’affichage de sa taille.

from PIL import Image
img = Image.open("joconde_1024.png")
img.show()
img.size

Principe de l’algorithme: On découpe l’image carrée en quatre quadrants, on fait tourner récursivement chaque quart, puis on opère une permutation circulaire des quadrants.

Méthode diviser pour régner appliquée à la rotation d’une image

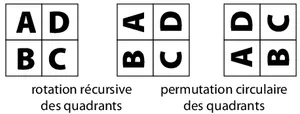
Pour tenter de faire cet exercice, vous pourrez utiliser la fonction echange_pixels qui permet d’échanger les valeurs des pixels de coordonnées x0, y0 et x1, y1.

def echange_pixels(image: PIL.image,
                   x0: int, y0: int,
                   x1: int, y1: int) -> PIL.image:
    couleurs0, couleurs1 = image.getpixel(x0, y0), image.getpixel(x1, y1)
    image.putpixel(x0, y0, couleurs1)
    image.putpixel(x1, y1, couleurs0)
    return image

À vous, bon courage!